TMfPOFD: Trimmed Mean for Partially Observed Functional Data
Bachelor's Thesis, University of Science and Technology of China, Mathematics Department,
Thesis
Overview
In this bachelor’s thesis, titled Trimmed Mean for Partially Observed Functional Data, we introduce the trimmed mean for partially observed functional data. We prove the robustness and strong consistency of this method. The work primarily references the following studies:
Integrated Depths for Partially Observed Functional Data
Authors: A. Elías, R. Jiménez, A. M. Paganoni, L. M. Sangalli
Journal: Journal of Computational and Graphical Statistics (2022)
DOI: 10.1080/10618600.2022.2070171Trimmed Means for Functional Data
Authors: Ricardo Fraiman, Graciela Muniz
Institutions: Universidad de San Andrés, Buenos Aires, Argentina & Universidad de la República, Montevideo, Uruguay
Year: May 2001
AMS 1980 Subject Classifications: 62G07, 62G05
DOI: 10.1007/BF02595706
Mathematical Definition
$$ \hat{\mu}_{n}(t) = \frac{\sum_{i=1}^{n} \mathbf{1}_{[\beta,+\infty)}\left(POIFD_{n}\left(X_{i}\right)\right) \mathbf{1}_{\text{observed}}\left(X_{i}(t)\right) X_{i}(t)}{\sum_{i=1}^{n} \mathbf{1}_{[\beta,+\infty)}\left(POIFD_{n}\left(X_{i}\right)\right) \mathbf{1}_{\text{observed}}\left(X_{i}(t)\right)} $$
where \(\beta\) satisfies:
$$ \frac{1}{n} \sum_{i=1}^{n} \mathbf{1}_{[\beta,+\infty)}\left(POIFD_{n}\left(X_{i}\right)\right) \approx 1-\alpha $$
where \(POIFD_{n}(X)\) is the Partially Observed Integrated Functional Depth of \(X\).You can also download the original thesis at Integrated Depths for Partially Observed Functional Data for more details.
Coding
The code for this thesis is available in the repository: TMoPOFD GitHub Repository. This repository contains the simulation code for the Trimmed Mean for Partially Observed Functional Data (TMoPOFD), based on the Partially Observed Integrated Functional Depth (POIFD) method.
The code aims to define the trimmed mean for partially observed functional data using the POIFD method and to establish the strong convergence of this estimator. Additionally, the code utilizes the package from the study Integrated Depths for Partially Observed Functional Data to generate POIFD-related work, which is available at https://github.com/aefdz/fdaPOIFD.
Usage Example
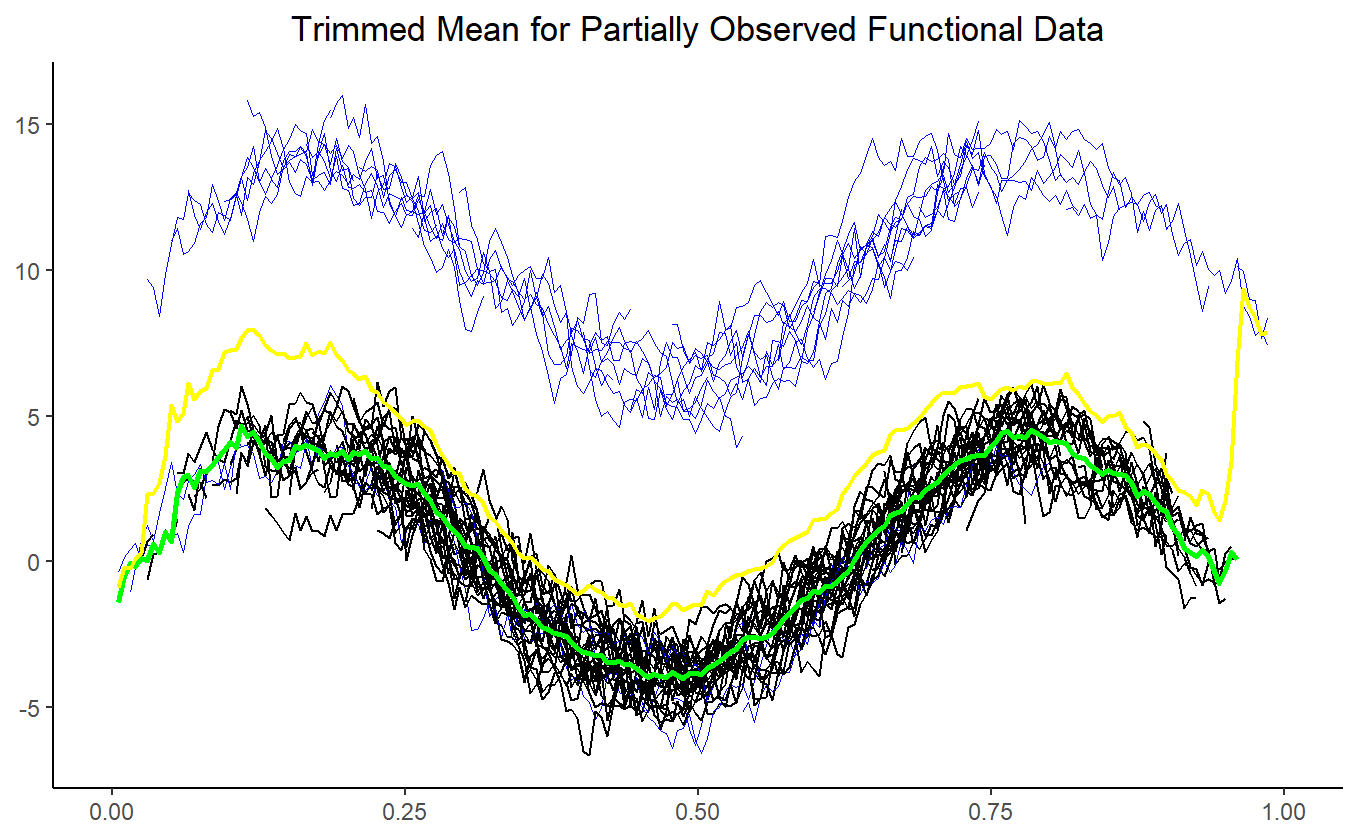
Below is an example of how to simulate data and plot the trimmed mean using this code:
# Simulate the data
SimulateModel <- simulateModel(
len = 200,
p = 50,
q = 0.3,
M = 10,
pollution_type = "asymmetric"
)
# Plot the data
plotTrimmedMean(data, alpha = 0.3, type = "FMD")
In the plot, the green line represents the trimmed mean, the yellow line represents the mean before trimming, and the blue lines represent the functions that were trimmed.